Opengl Draw Square on 3d Plane
Section 3.1
Shapes and Colors in OpenGL 1.1
This section introduces some of the cadre features of OpenGL. Much of the give-and-take in this department is express to 2nd. For at present, all you demand to know about 3D is that it adds a third direction to the 10 and y directions that are used in 2d. By convention, the third direction is calledz. In the default coordinate system, the x and y axes lie in the airplane of the paradigm, and the positive management of the z-centrality points in a direction perpendicular to the prototype.
In the default coordinate organisation for OpenGL, the image shows a region of 3D infinite in which x, y, and z all range from minus one to one. To prove a dissimilar region, y'all have to employ a transform. For now, we will simply employ coordinates that lie between -1 and i.
A annotation most programming: OpenGL can be implemented in many different programming languages, but the API specification more than or less assumes that the linguistic communication is C. (See Section A.2 for a brusque introduction to C.) For the nearly part, the C specification translates directly into other languages. The main differences are due to the special characteristics of arrays in the C linguistic communication. My examples will follow the C syntax, with a few notes nearly how things tin can be different in other languages. Since I'm post-obit the C API, I volition refer to "functions" rather than "subroutines" or "methods." Section 3.six explains in detail how to write OpenGL programs in C and in Java. You will need to consult that section before you lot tin do whatsoever bodily programming. The live OpenGL 1.1 demos for this volume are written using a JavaScript simulator that implements a subset of OpenGL 1.1. That simulator is discussed in Subsection 3.half-dozen.3.
3.1.1 OpenGL Primitives
OpenGL can describe just a few basic shapes, including points, lines, and triangles. There is no built-in back up for curves or curved surfaces; they must exist approximated past simpler shapes. The basic shapes are referred to as primitives. A primitive in OpenGL is defined by its vertices. A vertex is but a bespeak in 3D, given by its x, y, and z coordinates. Let'south jump right in and see how to draw a triangle. It takes a few steps:
glBegin(GL_TRIANGLES); glVertex2f( -0.seven, -0.5 ); glVertex2f( 0.7, -0.5 ); glVertex2f( 0, 0.7 ); glEnd();
Each vertex of the triangle is specified by a call to the role glVertex2f. Vertices must exist specified between calls to glBegin and glEnd. The parameter to glBegin tells which blazon of archaic is being drawn. The GL_TRIANGLES primitive allows you to describe more than one triangle: Only specify three vertices for each triangle that you desire to draw. Note that using glBegin/glEnd is non the preferred way to specify primitives, even in OpenGL i.ane. However, the culling, which is covered in Subsection 3.4.2, is more complicated to use. You should consider glBegin/glEnd to be a convenient style to larn about vertices and their properties, but not the way that you will actually do things in modern graphics APIs.
(I should annotation that OpenGL functions actually just ship commands to the GPU. OpenGL can save up batches of commands to transmit together, and the drawing won't actually be washed until the commands are transmitted. To ensure that that happens, the office glFlush() must be called. In some cases, this function might be called automatically past an OpenGL API, but yous might well meet times when you take to call it yourself.)
For OpenGL, vertices have three coordinates. The function glVertex2f specifies the x and y coordinates of the vertex, and the z coordinate is prepare to zippo. There is also a function glVertex3f that specifies all three coordinates. The "2" or "3" in the proper name tells how many parameters are passed to the function. The "f" at the end of the name indicates that the parameters are of type float. In fact, at that place are other "glVertex" functions, including versions that accept parameters of type int or double, with named like glVertex2i and glVertex3d. In that location are even versions that take four parameters, although it won't be clear for a while why they should exist. And, every bit we volition run into after, there are versions that have an array of numbers instead of private numbers equally parameters. The unabridged set of vertex functions is oftentimes referred to every bit "glVertex*", with the "*" standing in for the parameter specification. (The proliferation of names is due to the fact that the C programming language doesn't support overloading of function names; that is, C distinguishes functions just past their names and not by the number and type of parameters that are passed to the function.)
OpenGL 1.one has ten kinds of primitive. 7 of them even so be in mod OpenGL; the other three have been dropped. The simplest primitive is GL_POINTS, which simply renders a point at each vertex of the archaic. Past default, a point is rendered as a single pixel. The size of point primitives can exist changed past calling
glPointSize(size);
where the parameter, size, is of type float and specifies the diameter of the rendered bespeak, in pixels. By default, points are squares. You lot can become circular points by calling
glEnable(GL_POINT_SMOOTH);
The functions glPointSize and glEnable alter the OpenGL "country." The state includes all the settings that affect rendering. We will encounter many state-changing functions. The functions glEnable and glDisable can be used to turn many features on and off. In full general, the rule is that any rendering feature that requires extra computation is turned off by default. If you want that feature, you accept to turn it on by calling glEnable with the appropriate parameter.
There are three primitives for cartoon line segments: GL_LINES, GL_LINE_STRIP, and GL_LINE_LOOP. GL_LINES draws asunder line segments; specify two vertices for each segment that you want to draw. The other two primitives draw continued sequences of line segments. The only difference is that GL_LINE_LOOP adds an extra line segment from the terminal vertex back to the first vertex. Hither is what yous get if use the aforementioned six vertices with the four primitives we have seen and so far:
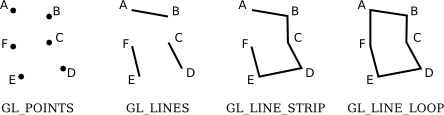
The points A, B, C, D, E, and F were specified in that order. In this illustration, all the points lie in the same plane, only continue in listen that in full general, points can exist anywhere in 3D space.
The width for line primitives can be gear up by calling glLineWidth(width). The line width is e'er specified in pixels. It is non subject to scaling past transformations.
Allow'due south look at an case. OpenGL does non have a circle archaic, simply we can estimate a circle by drawing a polygon with a big number of sides. To draw an outline of the polygon, nosotros can use a GL_LINE_LOOP primitive:
glBegin( GL_LINE_LOOP ); for (i = 0; i < 64; i++) { bending = 6.2832 * i / 64; // half-dozen.2832 represents 2*PI x = 0.5 * cos(bending); y = 0.five * sin(angle); glVertex2f( ten, y ); } glEnd(); This draws an approximation for the circumference of a circle of radius 0.five with center at (0,0). Recall that to learn how to apply examples like this 1 in a complete, running program, yous will have to read Department 3.6. Also, you might accept to make some changes to the code, depending on which OpenGL implementation you are using.
The next set of primitives is for drawing triangles. There are three of them: GL_TRIANGLES, GL_TRIANGLE_STRIP, and GL_TRIANGLE_FAN.
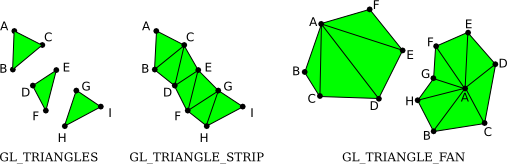
The three triangles on the left make up one GL_TRIANGLES primitive, with nine vertices. With that primitive, every set of iii vertices makes a split triangle. For a GL_TRIANGLE_STRIP archaic, the first 3 vertices produce a triangle. After that, every new vertex adds another triangle to the strip, connecting the new vertex to the 2 previous vertices. Two GL_TRIANGLE_FAN primitives are shown on the right. Again for a GL_TRIANGLE_FAN, the first iii vertices make a triangle, and every vertex after that adds anther triangle, but in this case, the new triangle is made by connecting the new vertex to the previous vertex and to the very first vertex that was specified (vertex "A" in the picture). Note that Gl_TRIANGLE_FAN can be used for cartoon filled-in polygons. In this moving-picture show, by the way, the dots and lines are not function of the archaic; OpenGL would only draw the filled-in, light-green interiors of the figures.
The three remaining primitives, which accept been removed from modern OpenGL, are GL_QUADS, GL_QUAD_STRIP, and GL_POLYGON. The name "quad" is short for quadrilateral, that is, a four-sided polygon. A quad is determined by four vertices. In club for a quad to be rendered correctly in OpenGL, all vertices of the quad must lie in the same plane. The aforementioned is truthful for polygon primitives. Similarly, to be rendered correctly, quads and polygons must be convex (see Subsection 2.2.three). Since OpenGL doesn't check whether these conditions are satisfied, the use of quads and polygons is fault-prone. Since the same shapes tin easily exist produced with the triangle primitives, they are not really necessary, merely here for the record are some examples:
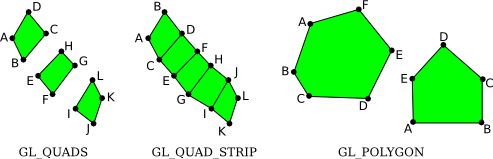
The vertices for these primitives are specified in the order A, B, C, .... Note how the gild differs for the two quad primitives: For GL_QUADS, the vertices for each individual quad should be specified in counterclockwise order around the quad; for GL_QUAD_STRIP, the vertices should alternate from one side of the strip to the other.
3.1.2 OpenGL Color
OpenGL has a large drove of functions that can exist used to specify colors for the geometry that we draw. These functions have names of the course glColor*, where the "*" stands for a suffix that gives the number and type of the parameters. I should warn you now that for realistic 3D graphics, OpenGL has a more than complicated notion of color that uses a different set of functions. You will learn about that in the next chapter, only for now we volition stick to glColor*.
For example, the role glColor3f has three parameters of type float. The parameters give the red, green, and bluish components of the color as numbers in the range 0.0 to 1.0. (In fact, values outside this range are immune, even negative values. When color values are used in computations, out-of-range values will be used as given. When a color really appears on the screen, its component values are clamped to the range 0 to 1. That is, values less than nada are changed to cipher, and values greater than one are changed to i.)
You tin can add together a fourth component to the color past using glColor4f(). The fourth component, known as blastoff, is not used in the default drawing manner, but it is possible to configure OpenGL to use information technology every bit the degree of transparency of the colour, similarly to the utilize of the alpha component in the 2D graphics APIs that we have looked at. You need ii commands to plow on transparency:
glEnable(GL_BLEND); glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
The starting time command enables use of the alpha component. It tin be disabled by calling glDisable(GL_BLEND). When the GL_BLEND option is disabled, blastoff is but ignored. The second control tells how the alpha component of a color will be used. The parameters shown here are the most common; they implement transparency in the usual way. I should note that while transparency works fine in 2nd, information technology is much more difficult to use transparency correctly in 3D.
If you would similar to use integer color values in the range 0 to 255, you can utilise glColor3ub() or glColor4ub to set the color. In these office names, "ub" stands for "unsigned byte." Unsigned byte is an viii-bit data type with values in the range 0 to 255. Here are some examples of commands for setting drawing colors in OpenGL:
glColor3f(0,0,0); // Draw in blackness. glColor3f(one,one,1); // Depict in white. glColor3f(ane,0,0); // Draw in total-intensity red. glColor3ub(1,0,0); // Describe in a color simply a tiny bit unlike from // black. (The suffix, "ub" or "f", is important!) glColor3ub(255,0,0); // Draw in full-intensity ruby-red. glColor4f(one, 0, 0, 0.5); // Draw in transparent red, but only if OpenGL // has been configured to do transparency. By // default this is the aforementioned as drawing in plain cerise.
Using any of these functions sets the value of a "current color," which is part of the OpenGL land. When you lot generate a vertex with ane of the glVertex* functions, the current color is saved along with the vertex coordinates, as an aspect of the vertex. We volition encounter that vertices can have other kinds of attribute as well as color. One interesting point about OpenGL is that colors are associated with individual vertices, not with complete shapes. By changing the electric current color between calls to glBegin() and glEnd(), you can get a shape in which different vertices have unlike color attributes. When you practice this, OpenGL will compute the colors of pixels inside the shape by interpolating the colors of the vertices. (Again, since OpenGL is extremely configurable, I take to note that interpolation of colors is only the default behavior.) For example, hither is a triangle in which the iii vertices are assigned the colors red, green, and blue:

This paradigm is ofttimes used as a kind of "Howdy World" example for OpenGL. The triangle can be drawn with the commands
glBegin(GL_TRIANGLES); glColor3f( 1, 0, 0 ); // red glVertex2f( -0.eight, -0.8 ); glColor3f( 0, one, 0 ); // light-green glVertex2f( 0.viii, -0.eight ); glColor3f( 0, 0, i ); // blue glVertex2f( 0, 0.nine ); glEnd();
Note that when cartoon a primitive, you do non demand to explicitly fix a color for each vertex, every bit was done here. If you want a shape that is all i color, y'all just take to set the current colour once, before drawing the shape (or just subsequently the call to glBegin(). For example, we tin draw a solid yellowish triangle with
glColor3ub(255,255,0); // yellow glBegin(GL_TRIANGLES); glVertex2f( -0.5, -0.5 ); glVertex2f( 0.5, -0.v ); glVertex2f( 0, 0.5 ); glEnd();
Also remember that the color for a vertex is specified before the call to glVertex* that generates the vertex.
Here is an interactive demo that draws the basic OpenGL triangle, with different colored vertices. You can control the colors of the vertices to run across how the interpolated colors in the interior of the triangle are afflicted. This is our showtime OpenGL instance. The demo actually uses WebGL, so you can employ information technology as a test to cheque whether your web browser supports WebGL.
The sample program jogl/FirstTriangle.java draws the basic OpenGL triangle using Java. The plan glut/first-triangle.c does the aforementioned using the C programming linguistic communication. And glsim/first-triangle.html is a version that uses my JavaScript simulator, which implements just the parts of OpenGL one.1 that are covered in this volume. Any of those programs could be used to experiment with 2D drawing in OpenGL. And you tin can apply them to exam your OpenGL programming environment.
A common functioning is to articulate the drawing area by filling it with some background colour. It is be possible to do that past drawing a big colored rectangle, but OpenGL has a potentially more efficient fashion to do it. The function
glClearColor(r,yard,b,a);
sets upward a color to exist used for immigration the drawing area. (This just sets the color; the color isn't used until you really give the control to articulate the cartoon area.) The parameters are floating point values in the range 0 to ane. There are no variants of this function; you must provide all four color components, and they must be in the range 0 to ane. The default clear colour is all zeros, that is, black with an blastoff component as well equal to zero. The control to do the bodily clearing is:
glClear( GL_COLOR_BUFFER_BIT );
The correct term for what I have been calling the drawing expanse is the color buffer, where "buffer" is a general term referring to a region in memory. OpenGL uses several buffers in add-on to the colour buffer. We volition run across the "depth buffer" in just a moment. The glClear command tin be used to articulate several different buffers at the same time, which can be more efficient than clearing them separately since the clearing can be washed in parallel. The parameter to glClear tells it which buffer or buffers to clear. To clear several buffers at once, combine the constants that stand for them with an arithmetic OR operation. For example,
glClear( GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT );
This is the form of glClear that is generally used in 3D graphics, where the depth buffer plays an essential role. For 2D graphics, the depth buffer is generally not used, and the advisable parameter for glClear is but GL_COLOR_BUFFER_BIT.
iii.1.3 glColor and glVertex with Arrays
We accept see that there are versions of glColor* and glVertex* that take different numbers and types of parameters. There are also versions that allow you place all the data for the command in a single array parameter. The names for such versions end with "v". For instance: glColor3fv, glVertex2iv, glColor4ubv, and glVertex3dv. The "v" really stands for "vector," pregnant substantially a ane-dimensional array of numbers. For example, in the role call glVertex3fv(coords), coords would exist an assortment containing at least three floating point numbers.
The being of array parameters in OpenGL forces some differences betwixt OpenGL implementations in dissimilar programming languages. Arrays in Java are different from arrays in C, and arrays in JavaScript are different from both. Let's await at the situation in C kickoff, since that'south the language of the original OpenGL API.
In C, assortment variables are a sort of variation on pointer variables, and arrays and pointers can be used interchangeably in many circumstances. In fact, in the C API, array parameters are really specified as pointers. For instance, the parameter for glVertex3fv is of type "pointer to float." The actual parameter in a call to glVertex3fv can exist an array variable, but information technology tin also be any arrow that points to the start of a sequence of 3 floats. As an example, suppose that we want to draw a foursquare. We need two coordinates for each vertex of the square. In C, we can put all 8 coordinates into 1 assortment and use glVertex2fv to pull out the coordinates that nosotros demand:
float coords[] = { -0.5, -0.five, 0.v, -0.5, 0.5, 0.five, -0.5, 0.5 }; glBegin(GL_TRIANGLE_FAN); glVertex2fv(coords); // Uses coords[0] and coords[1]. glVertex2fv(coords + 2); // Uses coords[2] and coords[iii]. glVertex2fv(coords + 4); // Uses coords[4] and coords[5]. glVertex2fv(coords + 6); // Uses coords[six] and coords[7]. glEnd(); This example uses "pointer arithmetics," in which coords + N represents a pointer to the N-th element of the array. An alternative note would be &coords[Northward], where "&" is the address operator, and &coords[Due north] means "a pointer to coords[North]". This volition all seem very alien to people who are simply familiar with Java or JavaScript. In my examples, I will avoid using pointer arithmetic, just I will occasionally use accost operators.
As for Coffee, the people who designed JOGL wanted to preserve the ability to pull data out of the middle of an assortment. Nonetheless, it's not possible to work with pointers in Java. The solution was to replace a pointer parameter in the C API with a pair of parameters in the JOGL API—i parameter to specify the assortment that contains the data and 1 to specify the starting index of the information in the array. For example, hither is how the square-drawing lawmaking translates into Java:
bladder[] coords = { -0.5F, -0.5F, 0.5F, -0.5F, 0.5F, 0.5F, -0.5F, 0.5F }; gl2.glBegin(GL2.GL_TRIANGLES); gl2.glVertex2fv(coords, 0); // Uses coords[0] and coords[one]. gl2.glVertex2fv(coords, 2); // Uses coords[2] and coords[three]. gl2.glVertex2fv(coords, 4); // Uses coords[4] and coords[5]. gl2.glVertex2fv(coords, vi); // Uses coords[6] and coords[seven]. gl2.glEnd(); In that location is really non much difference in the parameters, although the null in the outset glVertex2fv is a little annoying. The main deviation is the prefixes "gl2" and "GL2", which are required by the object-oriented nature of the JOGL API. I won't say more about JOGL here, only if y'all demand to translate my examples into JOGL, you should go on in mind the actress parameter that is required when working with arrays.
For the tape, hither are the glVertex* and glColor* functions that I will use in this book. This is not the complete set that is bachelor in OpenGL:
glVertex2f( ten, y ); glVertex2fv( xyArray ); glVertex2d( x, y ); glVertex2dv( xyArray ); glVertex2i( 10, y ); glVertex2iv( xyArray ); glVertex3f( x, y, z ); glVertex3fv( xyzArray ); glVertex3d( 10, y, z ); glVertex3dv( xyzArray ); glVertex3i( x, y, z ); glVertex3iv( xyzArray ); glColor3f( r, yard, b ); glColor3f( rgbArray ); glColor3d( r, g, b ); glColor3d( rgbArray ); glColor3ub( r, grand, b ); glColor3ub( rgbArray ); glColor4f( r, chiliad, b, a); glColor4f( rgbaArray ); glColor4d( r, g, b, a); glColor4d( rgbaArray ); glColor4ub( r, g, b, a); glColor4ub( rgbaArray );
For glColor*, keep in mind that the "ub" variations crave integers in the range 0 to 255, while the "f" and "d" variations require floating-point numbers in the range 0.0 to i.0.
3.i.4 The Depth Test
An obvious signal about viewing in 3D is that 1 object can exist behind another object. When this happens, the back object is subconscious from the viewer by the front end object. When we create an image of a 3D earth, we have to brand sure that objects that are supposed to be hidden backside other objects are in fact non visible in the image. This is the hidden surface problem.
The solution might seem elementary enough: Just depict the objects in social club from back to front. If 1 object is behind another, the back object will be covered upward later when the front end object is drawn. This is chosen the painter's algorithm. It's essentially what you are used to doing in second. Unfortunately, it's not so easy to implement. First of all, you lot can have objects that intersect, so that part of each object is hidden by the other. Any order yous describe the objects in, there will exist some points where the wrong object is visible. To fix this, you would have to cutting the objects into pieces, along the intersection, and treat the pieces as separate objects. In fact, there tin be problems fifty-fifty if there are no intersecting objects: Information technology's possible to take three non-intersecting objects where the first object hides function of the 2nd, the second hides part of the third, and the third hides part of the first. The painter's algorithm will fail regardless of the order in which the 3 objects are drawn. The solution again is to cut the objects into pieces, but now it's not and so obvious where to cut.
Even though these issues can be solved, at that place is another issue. The correct drawing order tin change when the betoken of view is changed or when a geometric transformation is applied, which means that the correct cartoon order has to exist recomputed every time that happens. In an animation, that would mean for every frame.
So, OpenGL does not employ the painter'southward algorithm. Instead, it uses a technique called the depth test. The depth test solves the hidden surface problem no matter what order the objects are fatigued in, then you can depict them in whatever order you desire! The term "depth" hither has to do with the distance from the viewer to the object. Objects at greater depth are further from the viewer. An object with smaller depth volition hide an object with greater depth. To implement the depth test algorithm, OpenGL stores a depth value for each pixel in the prototype. The extra retentiveness that is used to store these depth values makes upward the depth buffer that I mentioned earlier. During the drawing procedure, the depth buffer is used to keep track of what is currently visible at each pixel. When a 2d object is drawn at that pixel, the data in the depth buffer can be used to determine whether the new object is in front of or behind the object that is currently visible there. If the new object is in forepart, then the color of the pixel is changed to show the new object, and the depth buffer is also updated. If the new object is behind the current object, then the data for the new object is discarded and the color and depth buffers are left unchanged.
By default, the depth examination is non turned on, which can pb to very bad results when drawing in 3D. You lot can enable the depth examination by calling
glEnable( GL_DEPTH_TEST );
It can be turned off by calling glDisable(GL_DEPTH_TEST). If yous forget to enable the depth exam when drawing in 3D, the epitome that you get volition likely be confusing and will make no sense physically. Yous can besides get quite a mess if you forget to clear the depth buffer, using the glClear command shown earlier in this section, at the same time that you articulate the colour buffer.
Hither is a demo that lets y'all experiment with the depth examination. It also lets you see what happens when part of your geometry extends outside the visible range of z-values.
Hither are are a few details most the implementation of the depth test: For each pixel, the depth buffer stores a representation of the altitude from the viewer to the point that is currently visible at that pixel. This value is substantially the z-coordinate of the point, after any transformations accept been applied. (In fact, the depth buffer is frequently chosen the "z-buffer".) The range of possible z-coordinates is scaled to the range 0 to 1. The fact that there is only a limited range of depth buffer values ways that OpenGL can only display objects in a limited range of distances from the viewer. A depth value of 0 corresponds to the minimal distance; a depth value of one corresponds to the maximal distance. When you articulate the depth buffer, every depth value is ready to 1, which tin can be thought of as representing the background of the image.
You go to choose the range of z-values that is visible in the image, past the transformations that you apply. The default range, in the absence of whatsoever transformations, is -ane to 1. Points with z-values exterior the range are not visible in the image. It is a common problem to use too minor a range of z-values, so that objects are missing from the scene, or have their fronts or backs cut off, because they lie exterior of the visible range. You lot might be tempted to use a huge range, to make sure that the objects that you want to include in the paradigm are included within the range. Still, that'south not a good idea: The depth buffer has a limited number of bits per pixel and therefore a limited amount of accurateness. The larger the range of values that it must correspond, the harder it is to distinguish between objects that are almost at the same depth. (Call up about what would happen if all objects in your scene have depth values betwixt 0.499999 and 0.500001—the depth buffer might come across them all every bit beingness at exactly the same depth!)
There is another consequence with the depth buffer algorithm. It can requite some strange results when two objects have exactly the aforementioned depth value. Logically, it's not fifty-fifty clear which object should be visible, merely the real problem with the depth test is that information technology might show i object at some points and the second object at another points. This is possible because numerical calculations are not perfectly authentic. Hither an actual instance:

In the two pictures shown here, a gray square was drawn, followed by a white foursquare, followed by a black foursquare. The squares all prevarication in the aforementioned plane. A very small rotation was practical, to force the figurer do some calculations before drawing the objects. The flick on the left was drawn with the depth test disabled, so that, for example, when a pixel of the white foursquare was drawn, the estimator didn't try to figure out whether information technology lies in front of or behind the gray square; it but colored the pixel white. On the right, the depth examination was enabled, and yous can come across the strange result.
Finally, past the manner, note that the discussion here assumes that in that location are no transparent objects. Unfortunately, the depth examination does not handle transparency correctly, since transparency ways that two or more objects tin contribute to the colour of the pixel, just the depth test assumes that the pixel color is the color of the object nearest to the viewer at that point. To handle 3D transparency correctly in OpenGL, you pretty much have to resort to implementing the painter's algorithm past hand, at least for the transparent objects in the scene.
Source: https://math.hws.edu/graphicsbook/c3/s1.html
0 Response to "Opengl Draw Square on 3d Plane"
Post a Comment